| 1 |
|
The world is all that is the
case. |
| 1.1 |
|
The world is the totality of
facts, not of things. |
| 1.11 |
|
The world is determined by the
facts, and by their being all the facts. |
| 1.12 |
|
For the totality of facts
determines what is the case, and also whatever is not the case. |
| 1.13 |
|
The facts in logical space are
the world. |
| 1.2 |
|
The world divides into facts. |
| 1.21 |
|
Each item can be the case or not
the case while everything else remains the same. |
| 2 |
|
What is the case—a fact—is
the existence of states of affairs. |
| 2.01 |
|
A state of affairs (a state of
things) is a combination of objects (things). |
| 2.02 |
|
Objects are simple. |
| 2.03 |
|
In a state of affairs objects
fit into one another like the links of a chain. |
| 2.04 |
|
The totality of existing states
of affairs is the world. |
| 2.05 |
|
The totality of existing states
of affairs also determines which states of affairs do not exist. |
| 2.06 |
|
The existence and non-existence
of states of affairs is reality. |
| 2.1 |
|
We picture facts to ourselves. |
| 2.11 |
|
A picture presents a situation
in logical space, the existence and non-existence of states of
affairs. |
| 2.12 |
|
A picture is a model of reality. |
| 2.13 |
|
In a picture objects have the
elements of the picture corresponding to them. |
| 2.14 |
|
What constitutes a picture is
that its elements are related to one another in a determinate way. |
| 2.15 |
|
The fact that the elements of a
picture are related to one another in a determinate way represents
that things are related to one another in the same way.
Let us call this connexion of its
elements the structure of the picture, and let us call the possibility
of this structure the pictorial form of the picture. |
| 2.16 |
|
If a fact is to be a picture, it
must have something in common with what it depicts. |
| 2.17 |
|
What a picture must have in
common with reality, in order to be able to be able to depict
it—correctly or incorrectly—in the way it does, is its pictorial
form. |
| 2.18 |
|
What any picture, of whatever
form, must have in common with reality, in order to be able to depict
it—correctly or incorrectly—in any way at all, is logical form,
i.e. the form of reality. |
| 2.19 |
|
Logical pictures can depict the
world. |
| 2.2 |
|
A picture has logico-pictorial
form in common with what it depicts. |
| 2.21 |
|
A picture agrees with reality or
fails to agree, it is correct or incorrect, true or false. |
| 2.22 |
|
What a picture represents it
represents independently of its truth or falsity, by means of its
pictorial form. |
| 3 |
|
A logical picture of facts is a
thought. |
| 3.01 |
|
The totality of true thoughts is
a picture of the world. |
| 3.02 |
|
A thought contains the
possibility of the situation of which it is the thought. What is
thinkable is possible too. |
| 3.03 |
|
Thought can never be of anything
illogical, since, if it were, we should have to think illogically. |
| 3.04 |
|
If a thought were correct a
priori, it would be a thought whose possibility ensured its
truth. |
| 3.05 |
|
A priori knowledge that
a thought was true would be possible only if its truth were
recognizable from thought itself (without anything to compare it
with). |
| 3.1 |
|
In a proposition a thought finds
an expression that can be perceived by the senses. |
| 3.11 |
|
We use the perceptible sign of a
proposition (spoken or written, etc.) as a projection of a possible
situation. |
| 3.12 |
|
I call the sign with which we
express a thought a propositional sign—And a proposition is a
propositional sign in its projective relation to the world. |
| 3.13 |
|
A proposition includes all that
the projection includes, but not what is projected.
Therefore, though what is
projected is not itself included, its possibility is.
A proposition, therefore, does not
actually contain its sense, but does contain the possibility of
expressing it.
(‘The content of proposition’
means the content of a proposition that has sense.)
A proposition contains the form,
but not the content, of its sense. |
| 3.14 |
|
What constitutes a propositional
sign is that in it its elements (the words) stand in a determinate
relation to one another. |
| 3.2 |
|
In a proposition a thought can
be expressed in such a way that elements of the propositional sign
correspond to the objects of the thought. |
| 3.21 |
|
The configuration of objects in
a situation corresponds to the configuration of simple signs in the
propositional sign. |
| 3.22 |
|
In a proposition a name is the
representative of an object. |
| 3.23 |
|
The requirement that simple
signs be possible is the requirement that sense be determinate. |
| 3.24 |
|
A proposition about a complex
stands in an internal relation to a proposition about a constituent of
the complex.
A complex can be given only by its
description, which will be right or wrong. A proposition that mentions
a complex will not be nonsensical, if the complex does not exist, but
simply false.
When a propositional element
signifies a complex, this can be seen from an indeterminateness in the
propositions in which it occurs. In such cases we know that the
proposition leaves something undetermined. (In fact the notation for
generality contains a prototype.)
The contraction of a symbol for a
complex into a simple symbol can be expressed in a definition. |
| 3.25 |
|
A proposition has one and only
one complete analysis. |
| 3.26 |
|
A name cannot be dissected any
further by means of a definition: it is a primitive sign. |
| 3.3 |
|
Only propositions have sense;
only in the nexus of a proposition does a name have meaning. |
| 3.31 |
|
I call any part of propositions
that characterizes its sense an expression (or a symbol).
(A proposition is itself an
expression.)
Everything essential to their
sense that propositions can have in common with one another is an
expression.
An expression is the mark of a
form and a content. |
| 3.32 |
|
A sign is what can be perceived
of a symbol. |
| 3.33 |
|
In logical syntax the meaning of
a sign should never play a role. It must be possible to establish
logical syntax without mentioning the meaning of a sign: only
the description of expressions may be presupposed. |
|
|
. . . . . |
| 3.34 |
|
A proposition possesses
essential and accidental features.
Accidental features are those that
result from the particular way in which the propositional sign is
produced. Essential features are those without which the proposition
could not express its sense. |
|
|
. . . . . |
| 3.4 |
|
A proposition determines a place
in logical space. The existence of this logical place is guaranteed by
the mere existence of the constituents—by the existence of the
proposition with a sense. |
| 3.41 |
|
The propositional sign with
logical coordinates—that is the logical space. |
|
|
. . . . . |
| 3.42 |
|
A proposition can determine only
one place in logical space: nevertheless the whole of logical space
must already be given by it.
(Otherwise negation, logical sum,
logical product, etc., would introduce more and more new elements—in
coordination.)
(The logical scaffolding
surrounding a picture determines logical space. The force of a
proposition reaches through the whole of logical space.) |
| 3.5 |
|
A propositional sign, applied
and thought out, is a thought. |
| 4 |
|
A thought is a proposition with
a sense. |
|
|
. . . . . |
| 4.01 |
|
A proposition is a picture of
reality.
A proposition is a model of
reality as we imagine it. |
|
|
. . . . . |
| 4.02 |
|
We can see this from the fact
that we understand the sense of a propositional sign without its
having been explained to us. |
|
|
. . . . . |
| 4.03 |
|
A proposition must use old
expressions to communicate a new sense.
A proposition communicates a
situation to us, and so it must be essentially connected with the
situation.
And the connexion is precisely
that it is its logical picture.
A proposition states something
only in so far as it is a picture. |
|
|
. . . . . |
| 4.04 |
|
In a proposition there must be
exactly as many distinguishable parts as in the situation that it
represents.
The two must possess the same
logical (mathematical) multiplicity. (Compare Hertz’s Mechanics
on dynamical models.) |
|
|
. . . . . |
| 4.05 |
|
Reality is compared with
propositions. |
| 4.06 |
|
A proposition can be true or
false only in virtue of being a picture of reality. |
|
|
. . . . . |
| 4.1 |
|
Propositions represent the
existence and non-existence of states of affairs. |
| 4.11 |
|
The totality of true
propositions is the whole of natural science (or the whole corpus of
the natural sciences). |
|
|
. . . . . |
| 4.12 |
|
Propositions can represent the
whole of reality, but they cannot represent what they must have in
common with reality in order to be able to represent it—logical
form.
In order to be able to represent
logical form, we should have to be able to station ourselves with
propositions somewhere outside logic, that is to say outside the
world. |
|
|
. . . . . |
| 4.2 |
|
The sense of a proposition is
its agreement and disagreement with possibilities of existence and
non-existence of states of affairs. |
| 4.21 |
|
The simplest kind of
proposition, an elementary proposition, asserts the existence of a
state of affairs. |
| 4.211 |
|
It is a sign of a
proposition’s being elementary that there can be no elementary
proposition contradicting it. |
| 4.22 |
|
An elementary proposition
consists of names. It is a nexus, a concatenation, of names. |
| 4.23 |
|
It is only in the nexus of an
elementary proposition that a name occurs in a proposition. |
| 4.24 |
|
Names are the simple symbols: I
indicate them by single letters 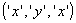 .
I write elementary propositions as functions of names, so that they
have the form .
I write elementary propositions as functions of names, so that they
have the form 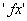 , , 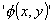 ,
etc. ,
etc.
Or I indicate them by the letters 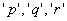 . . |
| 4.25 |
|
If an elementary proposition is
true, the state of affairs exists: if an elementary proposition is
false, the state of affairs does not exist. |
| 4.26 |
|
If all true elementary
propositions are given, the result is a complete description of the
world. The world is completely described by giving all elementary
propositions, and adding which of them are true and which false. |
| 4.27 |
|
For 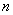 states of affairs, there are
states of affairs, there are
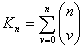 possibilities
of existence and non-existence. possibilities
of existence and non-existence.
Of these states of affairs any
combination can exist and the remainder not exist. |
| 4.28 |
|
There correspond to these
combinations the same number of possibilities of truth—and
falsity—for 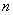 elementary
propositions. elementary
propositions. |
| 4.3 |
|
Truth-possibilities of
elementary propositions mean possibilities of existence and
non-existence of states of affairs. |
| 4.31 |
|
We can represent
truth-possibilities by schemata of the following kind (‘T’ means
‘true’, ‘F’ means ‘false’; the rows of ‘Ts’ and
‘Fs’ under the row of elementary propositions symbolize their
truth-possibilities in a way that can easily be understood):
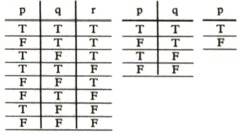
|
| 4.4 |
|
A proposition is an expression
of agreement and disagreement with truth-possibilities of elementary
propositions. |
| 4.41 |
|
Truth-possibilities of
elementary propositions are the conditions of the truth and falsity of
propositions. |
|
|
. . . . . |
| 4.42 |
|
For 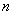 elementary propositions there are
elementary propositions there are
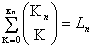 ways in which a proposition
can agree and disagree with their truth-possibilities. ways in which a proposition
can agree and disagree with their truth-possibilities. |
| 4.43 |
|
We can express agreement with
truth-possibilities by correlating the mark ‘T’ (true)
with them in the schema.
The absence of this mark means
disagreement. |
|
|
. . . . . |
| 4.44 |
|
The sign that results from
correlating the mark ‘T’ with truth-possibilities is a
propositional sign. |
|
|
. . . . . |
| 4.45 |
|
For 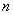 elementary propositions there are
elementary propositions there are 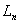 possible groups of truth-conditions.
possible groups of truth-conditions.
The groups of truth-conditions
that are obtainable from the truth-possibilities of a given number of
elementary propositions can be arranged in a series. |
| 4.46 |
|
Among the possible groups of
truth-conditions there are two extreme cases.
In one of these cases the
proposition is true for all the truth-possibilities of the elementary
propositions. We say that the truth-conditions are tautological.
In the second case the proposition
is false for all the truth-possibilities: the truth-conditions are contradictory.
In the first case we call the
proposition a tautology; in the second, a contradiction.
|
| 4.5 |
|
It now seems possible to give
the most general propositional form: that is, to give a description of
the proposition of any sign-language whatsoever in
such a way that every possible sense can be expressed by a symbol
satisfying the description, and every symbol satisfying the
description can express a sense, provided that the meanings of the
names are suitably chosen.
It is clear that only
what is essential to the most general propositional form may be
included in its description—for otherwise it would not be the most
general form.
The existence of a general
propositional form is proved by the fact that there cannot be a
proposition whose form could not have been foreseen (i.e.
constructed). The general form of a proposition is: This is how things
stand. |
| 4.51 |
|
Suppose that I am given all
elementary propositions: then I can simply ask what propositions I can
construct out of them. And there I have all propositions, and
that fixes their limits. |
| 4.52 |
|
Propositions comprise all that
follows from the totality of all elementary propositions (and, of
course, from its being the totality of them all).
(Thus, in a certain sense, it could be said that all
propositions were generalizations of elementary propositions.) |
| 4.53 |
|
The general propositional form
is a variable. |
| 5 |
|
A proposition is a
truth-function of elementary propostions.
(An elementary proposition is a
truth-function of itself.) |
| 5.01 |
|
Elementary propositions are the
truth-arguments of propostions. |
| 5.02 |
|
The arguments of functions are
readily confused with the affixes of names. For both arguments and
affixes enable me to recognize the meaning of the signs containing
them
For example, when Russell writes
'+c', the 'c' is an affix which indicates
that the sign as a whole is the addition-sign for cardinal numbers.
But the use of this sign is the result of arbitrary convention and it
would be quite possible to choose a simple sign instead of '+c';
in '~p', however, 'p' is not an affix but an
argument: the sense of '~p' cannot be understood
unless the sense of 'p' has been understood already. (In the
name Julius Caesar 'Julius' is an affix. An affix is always part of a
description of the object to whose name we attach it: e.g. the
Caesar of the Julian gens.)
If I am not mistaken, Frege's
theory about the meaning of propostions and functions is based on the
confusion between an argument and an affix. Frege regarded the
proposition of logic as names, and their arguments as the affixes of
those names. |
| 5.1 |
|
Truth-functions can be arranged
in series.
That is the foundations of the
theory of probability. |
| 5.101 |
|
The truth-functions of every
number of elementary propostions can be written in a schema of the
following kind:
 Those
truth-functions of its truth-arguments, which verify the propostion, I
shall call its truth-grounds. Those
truth-functions of its truth-arguments, which verify the propostion, I
shall call its truth-grounds. |
| 5.11 |
|
If all the truth-grounds that
are common to a number of propostions are at the same time
truth-grounds of a certain propostion, then we say that the truth of
that proposition follows from the truth of the others. |
| 5.12 |
|
In particular, the truth of a
propostion 'p' follows from the truth of another propostion 'q'
if all the truth-grounds of the latter are truth-grounds of the
former. |
| 5.121 |
|
The truth-grounds of 'q'
are contained in those of 'p'; 'p' follows from 'q'. |
| 5.122 |
|
If 'p' follows from 'q',
the sense of 'p' is contained in that of 'q'. |
| 5.123 |
|
If a god creates a world in
which certain propostions are true, he creates thereby also a world in
which all propositions consequent on them are true. And similarly he
could not create a world in which the propostion 'p' is true
without creating all its objects. |
| 5.124 |
|
A proposition asserts every
propostion which follows from it. |
| 5.13 |
|
When the truth of one
proposition follows from the truth of others, we can see this from the
structure of the propositions. |
| 5.133 |
|
All inference takes place a
priori. |
| 5.134 |
|
From an elementary proposition
no other can be inferred. |
| 5.135 |
|
In no way can an inference be
made from the existence of another entirely different from it. |
| 5.136 |
|
There is no causal nexus which
justifies such an inference. |
| 5.14 |
|
If one proposition follows from
another, then the latter says more than the former, and the former
less than the latter. |
| 5.15 |
|
If Tr is the
number of the truth-grounds of a proposition 'r', and if Trs
is the number of the truth-grounds of a proposition 's' that
are at the same time truth-grounds of 'r', then we call the
ratio Trs : Tr the degree of probability
that the proposition 'r' gives to the proposition 's'. |
| 5.2 |
|
The structures of propositions
stand in internal relations to one another. |
| 5.21 |
|
In order to give prominence to
these internal relations we can adopt the following mode of
expression: we can represent a proposition as the result of an
operation that produces it out of other propositions (which are the
bases of the operation). |
| 5.22 |
|
An operation is the expression
of a relation between the structures of its result and of its bases. |
| 5.23 |
|
The operation is what has to be
done to the one proposition in order to make the other out of it. |
| 5.24 |
|
An operation manifests itself in
a variable; it shows how we can get from one form of proposition to
another.
It gives expression to the
difference between the forms.
(And what the bases of an
operation and its result have in common is just the bases themselves.) |
| 5.25 |
|
The occurrence of an operation
does not characterize the sense of a proposition.
Indeed, no statement is made by an
operation, but only by its result, and this depends on the bases of
the operation.
(Operations and functions must not
be confused with each other.) |
| 5.3 |
|
All propositions are results of
truth-operations on elementary propositions.
A truth-operation is the way in
which a truth-function is produced out of elementary propositions.
It is the essence of
truth-operations that, just as elementary propositions yield a
truth-function of themselves, so too in the same way truth-functions
yield a further truth-function. When a truth-operation is applied to
truth-functions of elementary propositions, it always generates
another truth-function of elementary propositions, another
proposition. When a truth-operation is applied to the result of
truth-operations on elementary propositions, there is always a single
operation on elementary propositions that has the same result.
Every proposition is the result of
truth-operations on elementary propositions. |
| 5.31 |
|
The schemata in 4.31 have a
meaning even when 'p', 'q', 'r', etc. are
not elementary propositions.
And it is easy to see that the
propositional sign in 4.42 expresses a single truth-function of
elementary propositions even when 'p' and 'q' are
truth-functions of elementary propositions. |
| 5.32 |
|
All truth-functions are results
of successive applications to elementary propositions of a finite
number of truth-operations. |
| 5.4 |
|
At this point it becomes
manifest that there are no 'logical objects' or 'logical constants'
(in Frege's and Russell's sense). |
| 5.41 |
|
The reason is that the result of
truth-operations on truth-functions are always identical whenever they
are one and the same truth-function of elementary propositions. |
| 5.42 |
|
It is self-evident that that v, 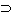 ,
etc. are not relations in the sense in which right and left etc. are
relations. ,
etc. are not relations in the sense in which right and left etc. are
relations.
The interdefinability of Frege's
and Russell's 'primitive signs' of logic is enough to show that they
are not primitive signs, still less signs for relations.
And it is obvious that the '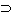 '
defined by means of '~' and 'v' is identical with the one that figures
with '~' in the definition of 'v': and that the second 'v' is
identical with the first one; and so on. '
defined by means of '~' and 'v' is identical with the one that figures
with '~' in the definition of 'v': and that the second 'v' is
identical with the first one; and so on. |
| 5.43 |
|
Even at first sight it seems
scarcely credible that there should follow from one fact p
infinitely many others, namely ~~p, ~~~~p,
etc. And it is no less remarkable that the infinite number of
propositions of logic (mathematics) follow from half a dozen
'primitive propostions'.
But in fact all propositions of
logic say the same thing, to wit nothing. |
| 5.44 |
|
Truth-functions are not material
functions.
For example, an affirmation can be
produced by double negation: in such a case does it follow that in
some sense negation is contained in affirmation? Does '~~p'
negate ~p, or does it affirm p--or both?
The proposition '~~p' is
not about negation, as if negation were an object: on the other hand,
the possibility of negation is already written into affirmation.
And if there were an object called
'~', it would follow that '~~p' said something different from
what 'p' said, just because the one proposition would then be
about ~ and the other would not. |
| 5.45 |
|
If there are primitive logical
signs, then any logic that fails to show clearly how they are placed
relatively to one another and to justify their existence will be
incorrect. The construction of logic out of its primitive
signs must be made clear. |
| 5.46 |
|
If we introduced logical signs
properly, then we should also have introduced at the same time the
sense of all combinations of them; i.e. not only 'p v q'
but '~(p v ~q)' as well, etc. etc. We should also
have introduced at the same time the effect of all possible
combinations of brackets. And thus it would have been made clear that
the real general primitive signs are not 'p v q', '(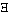 x).fx',
etc. but the most general form of their combinations. x).fx',
etc. but the most general form of their combinations. |
| 5.47 |
|
It is clear that whatever we can
say in advance about the form of all propositions we must be
able to say all at once.
An elementary proposition really
contains all logical operations in itself. For 'fa' says the
same as '(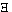 x).fx.x
= a'. x).fx.x
= a'.
Wherever there is compositeness,
argument and function are present, and where these are present, we
already have all the logical constants.
One could say that the sole
logical constant was what all propositions, by their very
nature, had in common with one another.
But that is the general
propositional form. |
| 5.5 |
|
Every truth-function is a result
of successive applications to elementary propositions of the operation
'(-----T)(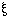 ,....)'. ,....)'.
This operation negates all the
propositions in the right-hand pair of brackets, and I call it the
negation of those propositions. |
| 5.51 |
|
If 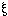 has only one value, then N(
has only one value, then N(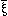 )
= ~p (not p); if it has two values, then N( )
= ~p (not p); if it has two values, then N(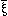 = ~p.~q (neither p nor q).
= ~p.~q (neither p nor q). |
| 5.52 |
|
If 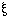 has as its values all that values of a function fx for all
values of x, then N(
has as its values all that values of a function fx for all
values of x, then N(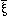 )=~( )=~(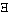 x).fx.
x).fx. |
| 5.53 |
|
Identity of the object I express
by identity of sign, and not by using a sign for identity. Difference
of objects I express by difference of signs. |
| 5.54 |
|
In the general propositional
form propostions occur in other propositions only as bases of
truth-operations. |
| 5.55 |
|
We now have to answer a priori
the question about all the possible forms of elementary propositions.
Elementary propositions consist of
names. Since, however, we are unable to give the number of names with
different meanings, we are also unable to give the composition of
elementary propostions. |
| 5.6 |
|
The limits of my language
mean the limits of my world. |
| 5.61 |
|
Logic pervades the world; the
limits of the world are also its limits.
So we cannot say in logic, 'The
world has this in it, and this, but not that.'
For that would appear to
presuppose that we were excluding certain possibilities, and this
cannot be the case, since it would require that logic should go beyond
the limits of the world; for only in that way could it view those
limits from the other side as well.
We cannot think what we cannot
think; so what we cannot think we cannot say either. |
| 5.62 |
|
This remark provides the key to
the problem, how much truth there is in solipsism.
For what the solipsist means
is quite correct; only it cannot be said, but makes itself
manifest.
The world is my world:
this is manifest in the fact that the limits of language (of
that language which alone I understand) mean the limits of my
world. |
| 5.63 |
|
I am my world. (The microcosm.) |
| 5.64 |
|
Here it can be seen that
solipsism, when its implications are followed out strictly, coincides
with pure realism. The self of solipsism shrinks to a point without
extension, and there remains the reality co-ordinated with it. |
| 6 |
|
The general form of a
truth-function is [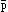 , , 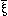 ,
N, ( ,
N, (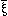 )]. This is the
general form of a proposition. )]. This is the
general form of a proposition. |
| 6.1 |
|
The propositions of logic are
are tautologies. |
| 6.11 |
|
Therefore the propositions of
logic say nothing. (They are the analytic propositions.) |
| 6.12 |
|
The fact that the propositions
of logic are tautologies shows the
formal--logical--properties of language and the world.
The fact that a tautology is
yielded by this particular way of connecting its
constituents.
If propositions are to yield a
tautology when they are connected in a certain way, they must have
certain structural properties. So their yielding a tautology when
combined in this way shows that they possess these structural
properties. |
| 6.13 |
|
Logic is not a body of doctrine,
but a mirror-image of the world.
Logic is transcendental. |
| 6.2 |
|
Mathematics is a logical method.
The propositions of mathematics
are equations, and therefore pseudo-propositions. |
| 6.21 |
|
A proposition of mathematics
does not express a thought. |
| 6.22 |
|
The logic of the world, which is
shown in tautologies by the propositions of logic, is shown in
equations by mathematics. |
| 6.23 |
|
If two expressions are combined
by means of the sign of equality, that means that they can be
substituted for one another. But it must be manifest in the two
expressions themselves whether this is the case or not.
When two expressions can be
substituted for one another, that characterizes their logical form. |
| 6.24 |
|
The method by which mathematics
arrives at its equations is the method of substitution.
For equations the substitutability
of two expressions and, starting from a number of equations, we
advance to new equations by substituting different expressions in
accordance with the equations. |
| 6.3 |
|
The exploration of logic means
the exploration of everything that is subject to law. And
outside logic everything is accidental. |
| 6.31 |
|
The so-called law of induction
cannot possibly be a law of logic, since it is obviously a proposition
with sense.--Nor, therefore, can it be an a priori law. |
| 6.32 |
|
The law of causality is not a
law but the form of a law. |
| 6.33 |
|
We do not have an a priori belief
in a law of conservation, but rather a priori knowledge of
the possibility of a logical form. |
| 6.34 |
|
All such propositions, including
the principle of sufficient reason, the laws of continuity in nature
and of least effort in nature, etc. etc.--all these are a priori
insights about the forms in which the propositions of science can be
cast. |
| 6.35 |
|
Although the spots in our
picture are geometrical figures, nevertheless geometry can obviously
say nothing at all about their actaul form and position. The network,
however, is purely geometrical; all its properties can be
given a priori.
Laws like the principle of
sufficient reason, etc. are about the net and not about what the net
describes. |
| 6.36 |
|
If there were a law of
causality, it might be put in the following way: There are laws of
nature.
But of course that cannot be said:
it makes itself manifest. |
| 6.37 |
|
There is no compulsion making
one thing happen because another has happened. The only necessity that
exists is logical necessity. |
| 6.4 |
|
All propositions are of equal
value. |
| 6.41 |
|
The sense of the world must lie
outside the world. In the world everything is as it is, and everything
happens as it does happen: in it no value exists--and if it
did exist, it would have no value.
If there is any value that does
have value, it must lie outside the whole sphere of what happens and
is the case. For all that happens and is the case is accidental.
What makes it non-accidental
cannot lie within the world, since if it did it would itself
be accidental.
It must lie outside the world. |
| 6.42 |
|
So too it is impossible for
there to be propositions of ethics.
Propositions can express nothing
that is higher. |
| 6.43 |
|
If the good or bad exercise of
the will does alter the world, it can alter only the limits of the
world, not the facts--not what can be expressed by means of language.
In short the effect must be that
it becomes an altogether different world. It must, so to speak, was
and wane as a whole.
The world of the man is a
different one from that of the unhappy man. |
| 6.44 |
|
It is not know things
are in the world that is mystical, but that it exists. |
| 6.45 |
|
To view the world sub specie
aeterni1 is to view it as a whole--a limited whole.
Feeling the world as a limited
whole--it is this that is mystical. |
| 6.5 |
|
When the answer cannot be put
into words, neither can the question be put into words.
The riddle does not
exist.
If a question can be framed at
all, it is also possible to answer it. |
| 6.51 |
|
Scepticism is not
irrefutable, but obviously nonsensical, when it tries to raise doubt
where no question can be asked.
For doubt can exist only where a
question exists, a question only where an answer exists, and an answer
only where something can be said. |
| 6.52 |
|
We feel that even when all possible
scientific questions have been answered, the problems of life remain
completely untouched. Of course there are then no questions left, and
this itself is the answer. |
| 6.53 |
|
The correct method in philosophy
would really be the following: to say nothing except what can be said,
i.e. propositions of natural science--i.e. something that has nothing
to do with philosophy--and then, whenever someone else wanted to say
something metaphysical, to demonstrate to him that he had failed to
give a meaning to certain signs in his propositions. Although it would
not be satisfying to the other person--he would not have the feeling
that we were teaching him philosophy--this method would be
the only strictly correct one. |
| 6.54 |
|
My propositions serve as
elucidations in the following way: anyone who understands me
eventually recognizes them as nonsensical, when he has used them--as
steps--to climb up beyond them. (He must, so to speak, throw away the
ladder after he has climbed up it.)
He must transcend these
propositions, and then he will see the world aright. |
| 7 |
|
What we cannot speak about we
must pass over in silence. |