|
One Hundred
Tamils of the 20th Century
Srinivasa Ramanujan
22
December 1887 - 26 April 1920
"An equation has no meaning for
me unless it expresses a thought of God"
- Srinivasa Iyengar Ramanujan
from a
stamp issued by India to commemorate
the 75th anniversary of Ramunujan's
birth
 Srinivasa Aiyangar Ramanujan was born
on 22 December 1887 in Erode, Tamil Nadu and died
at the early age of 33 on 26 April 1920 in
Kumbakonam. Ramanujan was one of the world's great
mathematicians. He made substantial contributions
to the analytical theory of numbers and worked on
elliptic functions, continued fractions, and
infinite series. Srinivasa Aiyangar Ramanujan was born
on 22 December 1887 in Erode, Tamil Nadu and died
at the early age of 33 on 26 April 1920 in
Kumbakonam. Ramanujan was one of the world's great
mathematicians. He made substantial contributions
to the analytical theory of numbers and worked on
elliptic functions, continued fractions, and
infinite series.
Ramanujan, was largely self-taught in
mathematics. He was given a fellowship to the
University of Madras in 1903 but the following year
he lost it because he devoted all his time to
mathematics and neglected his other subjects. He
married in 1909.
After publication of a brilliant research paper
on Jacob Bernoulli's numbers in 1911 in the Journal
of the Indian Mathematical Society his work gained
recognition.
His papers were sent to several English
mathematicians and Professor G H Hardy in Trinity College,
Cambridge was quick to recognise Raminujan's
genius. In 1914 Hardy invited Ramanujan to Trinity
College, Cambridge, to begin an extraordinary
collaboration. He sailed from India on 17 March
1914.
Ramanujan worked out the Riemann series, the
elliptic integrals, hyper geometric series and
functional equations of the zeta function.
Ramanujan independently discovered the results of
Gauss, Kummer and others on hyper geometric series.
Ramanujan's own work on partial sums and products
of hyper geometric series have led to major
development in the topic. He was admitted as a
Fellow of the Royal Society, though a Fellowship
at Trinity College, Cambridge somehow eluded
him.
He fell ill in 1917 and spent some time in
nursing homes. After a slight improvement in his
health, he sailed to India on 27 February 1919 and
died there the following year.
Ramanujan left a number of unpublished notebooks
filled with theorems that mathematicians have
continued to study. Hardy passed on to G.N.Watson,
Mason Professor of Pure Mathematics at Birmingham,
the large number of manuscripts of Ramanujan that
he had, both written before 1914 and some written
in Ramanujan's last year in India before his
death.
Watson published 14 papers under the general
title 'Theorems stated by Ramanujan' and in all
published nearly 30 papers which were inspired by
Ramanujan's work.
 C.J.Eliezer on
Ramanujan the Mathematician C.J.Eliezer on
Ramanujan the Mathematician
[see also C.J.Eliezer - One Hundred Tamils of
20th Century]
from a presentation at
the First International Tamil Conference
1966 - Kuala Lumpur, Malaysia
The history of mathematics bears the imprint of
many personalities of genius - of intellectual
giants with unusual abilities and uncanny insights.
Archimedes and Pythagoras. Newton and Lagrange.
Descartes and Gauss, Euler and Einstein-were among
the greatest of men. Intellectual passion and
romance. discoveries and great moments of history
have been associated with their names.
Among the exciting and unusual figures among the
great creators of mathematics is Srinivasa
Ramanujan, whose short life (1887 - 1920) had the
stamp of genius and greatness though perhaps
mingled with sadness and tragedy.
As one reflects on the life Ramanujan a thought
that comes to mind is the possibility that his
capabilities might well have gone unrecognised and
opportunity may not have come his way for the
growth and development of his talents. The help and
encouragement of various men of influence who were
themselves lovers of mathematics played an
important role in the early days of frustration and
uncertainty.
One such person was Diwan Bahadur Ramachandra
Rao, Collector at Nellore, who recalled in the
following words his first interview with Ramanujan
in 1910, when the latter was a twenty-two year old
youngster. (He had by then left College. having
failed in English in the First in Arts examination.
lost his scholarship and was without a job)
"A nephew of mine perfectly innocent of
mathematical knowledge said to me: 'Uncle, I have
a visitor who talks of mathematics: I do not
understand him; can you see if there is anything
in his talk'. And in the plenitude of my
mathematical wisdom, I condescended to permit
Ramanujan to walk into my presence A short figure
. . . with one conspicuous feature-shining eyes
---- walked in with a frayed notebook under his
arm. He was miserably poor . He had run away from
Kumabakonam to get leisure in Madras to pursue
his studies...
He opened his hook and began to explain some
of' his discoveries. I saw quite at once that
there was something out of the way: but my
knowledge did not permit me to judge whether he
talked sense or nonsense. Suspending judgement I
asked him to come over again, and he did. And
then he had gauged my ignorance and showed me
some of his simpler results. These transcended
existing books and I had no doubt that he was a
remarkable man. Then, step by step, he led me to
elliptic integrals and hyper geometric series and
at last to his theory of divergent series not yet
announced to the world converted me "
The reaction of Mr. Rao was typical of the
admiration which lovers of mathematics gradually
come to feel for Ramanujan's abilities and aroused
their desire to make it possible for hint to
continue with his mathematical pursuits. It would
seem that there was in his environment an
intellectual climate of appreciation of
mathematical science, and a spontaneous affection
and admiration for those who showed special
mathematical talents. Such an emphasis reflects a
traditional feature of Tamil society.
Among the first couplets of poetry which
generations of children lisped were from the
beloved and wise Avvaiyar:
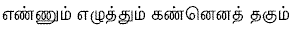
And earlier in the second century Thiruvalluvar
had said in Kura1 392
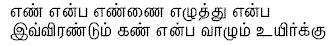
which may be rendered in English:
Numbers and letters -
these are the twin eyes of the mind.
The inventionof the number zero in India, and
the coming into use there of the present number
system had accelerated the progress of number
studies. And, over the centuries a love for
mathematics, expressed in songs and poems and
mathematical riddles (such as those which Thennali
Raman had enunciated), had been nurtured in that
society.
The phenomenon of Ramanujan gradually came to
the notice also of certain British civil servants
in India. These were mostly university men with a
background of liberal education. Their support and
enthusiasm were to play an important role on
Ramanujan's future. While Ramanujan was working as
an office clerk in the Madras Port Authority, his
mathematical talents were brought to the attention
of the Chairman of this body. This Chairman took
advantage of the visit to Madras of Dr. T. G.
Walker, F.R.S., Director-General of Observatories,
Simla, to show him some of Ramanujan's mathematical
works. The result was a persuasive letter from Dr.
Walker to the University of Madras in the following
terms:
" . . . the character of the work that I saw
impressed me as comparable in originality with
that of a mathematical fellow in a Cambridge
college ... the university would be justified in
enabling S. Ramanujan for a few years to spend
the whole of his time on Mathematics. without
anxiety, as to his livelihood."
Dr. Walker as a former fellow of Trinity
College. Cambridge, had known the value of the
system of research fellowships at Cambridge where
persons of promise are enabled to stay on at the
university and devote their full time to research,
without other dukes being required from them. The
existence of such fellowships is today a valuable
feature in universities which place emphasis on
research and new learning.
The University of Madras went out of their
normal provisions and awarded a special scholarship
to Ramanujan thus enabling him to give up his
clerkship and devote his full time to
mathematics.
In the meantime, at the suggestion of a former
teacher, Ramanujan began a correspondence with G.
H. Hardy at Trinity College, Cambridge. Hardy later
became for many decades the acknowledged leader of
British mathematics. In his first letter Ramanujan
wrote:
" . . . I had no university education. but I
have undergone the ordinary school course. After
leaving school I have been employing the spare
time at my disposal to work at Mathematics...
Very recently I came across a tract published by
you styled "Orders of Infinity`', in page 36 of
which I find a statement that no definite
expression has been as yet found for the number
of prime numbers less than any given number. I
have found an expression which very nearly
approximates to the real result.... I would
request you to go through the enclosed papers
...."
The papers enclosed contained enunciations of a
hundred or more mathematical theorems. Hardy was
amazed. He replied promptly in friendly and
encouraging terms. He further urged that Ramanujan
should enter Cambridge where with contact with many
mathematicians his talents would find ample scope
for creative mathematics. At first, Ramanujan would
not entertain the idea of going abroad owing to his
rigid observances of caste. Early in 1914 when a
fellow of Trinity E.H. Neville. was invited by the
University of Madras to visit and deliver some
mathematics courses he was given by Hardy the task
of persuading Ramanujan to go to Cambridge. This
Neville did successfully. Neville further proposed
to the University of Madras to award Ramanujan a
scholarship to proceed to Cambridge:
'The discovery of the genius of' S. Ramanujan
of Madras promises to be the most interesting
event of our time in the mathematical world... I
see no reason to doubt that Ramanujan himself
will respond fully to the stimulus which contact
with western mathematicians of the highest class
will afford him. In that case his name will
become one of the greatest in the history of
mathematics and the University and the City of
Madras will be proud to have assisted in his
passage from obscurity to fame.''
The university responded and Ramanujan reached
Cambridge in April 1914 in the company of Neville.
There Hardy and Littlewood introduced him to new
branches of mathematics, helped him to present his
work in the form of papers suitable for publication
in mathematical journals, and under their guidance
his mathematical talents developed rapidly.
Hardy has commented on the difficulties of
creating in Ramanujan the attitude of rigour
characteristic of modern mathematics
'The limitations of his knowledge were as
startling as its profundity. Here was a man who
could work out modular equations. and theorems of
complex multiplication to orders unheard of,
whose mastery of continued fractions was. on the
formal side at any rate beyond that of any
mathematician in the world, who had found for
himself the functional equation of the
Zeta-function, and the dominant terms in many of
the most famous problems in the analytic theory
of numbers; and he had never heard of a doubly
periodic function or of Cauchy's theorem, and had
indeed but the vaguest idea of what a function of
a complex variable was. His ideas of what
constituted a mathematical proof were of the most
shadowy description. All his results, new or old,
right or wrong, had been arrived at by a process
of mingled argument, intuition and
induction...
So I had to try to teach him. and in a measure
I succeeded. Though obviously I learnt from him
much more than he learnt from me. His flow of
original ideas showed no symptom of abatement
"
Again:
"Of his extraordinary gifts there can be no
question; in some ways he is the most remarkable
mathematician I have ever known"
Ramanujan's uncanny intuition was his special
asset Many of his results were so complicated that
expert mathematicians had to put in great effort to
provide acceptable proofs, and there still remain
unproved results. Even in his younger days, on
rising from bed. he would frequently jot down in
his famous note book some formula which he would
proceed to verify, though he was unable to supply a
proof. He would say that the goddess of Nammakkal
had inspired him with the formula during his sleep
It would be of interest to speculate if his
intuition would have remained as fertile if he had
gone through a proper mathematical discipline of
training. It could well be that systematic
education sometimes tends to limit the intuitive
capacities of children. In these days of mass
education, where children are taught in large
groups, the need for teachers to provide for the
special talents of each child, especially in the
case of mathematical talents, is important and
worth greater attention than is given at
present.
One of the happy features of Ramanujan's life at
Cambridge had been the affection and regard in
which Hardy, Littlewood, Neville and other
mathematicians held him, reminding us of the
international fraternity of mathematicians, who
irrespective of origins of race, background and
upbringing, are held together by a strong emotional
basic loyalty which transcends the many
differences.
Professor D. E. Daykin, my colleague in the
University of Malaya tells me that a few years ago
he attended a lecture by Prof. Neville on the life
of Ramanujan. During most of the lecture, tears
streamed down the cheeks of Prof. Neville. Among
other incidents, Neville referred to the occasion
when Ramanujan had borrowed some rare book from him
and accidentally some water had poured on the book.
Ramanujan was most unhappy, had written to several
dealers in rare books, and succeeded in obtaining
another copy. and with much apology he came to
Neville and gave him the two copies, with an
explanation of what had happened.
Ramanujan was in England for a little less than
five years. Parts of the last two years were alas,
in sanatoria, to arrest a tubercular tendency.
There were periods of improvement, convalescence
and relapse. But the mathematical activity
continued. His work began to receive public
recognition. He was elected to the Fellowship of
the Royal Society.
On one occasion when Hardy visited him in
hospital. the conversation casually went to the
subject of the number of the taxicab in which he
had travelled. Hardy remarked that the number was
1729 = 7 x 13 x 19 and thought that it was a dull
number. Ramanujan however said that it was a very
interesting number, being the smallest number
expressible as a sum of two cubes in two different
ways. So intimate was Ramanujan's knowledge about
the different numbers. Littlewood once
remarked that to Ramanujan every integer was a
personal friend.
The climate of England was not helping his
recovery, and his colleagues sadly planned his
return to India. It was anticipated that he would
fully recover in India's climate. The University of
Madras made various financial provisions. and was
contemplating the creation of a special
Professorship for him. He was disturbed that his
illness was preventing him from doing enough
mathematics to justify his scholarship. He wrote to
the University of Madras:
"I feel, however. that after my return to
India, which I expect to happen as soon as
arrangements can be made the total amount of
money to which I shall be entitled will be much
more than I shall require and I should hope that
after my expenses in England have been paid,
£50 a year will be paid to my parents and
that the surplus after my necessary expenses are
met should be used for some educational purpose
such in particular as the reduction of school
fees for poor boys and orphans and provision of
books in school.. .
I feel very sorry that. as I have not been
well, I have not been able to do much mathematics
during the last two years as before. I hope that
I shall soon he able to do more and will
certainly do my best to deserve the help that has
been given me."
Ramanujan returned to Madras in April 1919.
Respite best medical attention and the loving care
of friends, his health did not improve. He died in
April 20, at the age of 33, remaining
mathematically active right to the end with a
serenity of mind 'that held acquaintance with the
stars undisturbed by space and time.'
References
Biography in Dictionary of Scientific
Biography (New York 1970-1990).
Biography in Encyclopaedia Britannica.
G H Hardy, Ramanujan (Cambridge, 1940).
R Kanigel, The man who knew infinity : A life of
the genius Ramanujan (New York, 1991).
S Ram, Srinivasa Ramanujan (New Delhi, 1979).
S R Ranganathan, Ramanujan : the man and the
mathematician (London, 1967).
B Berndt, Srinivasa Ramanujan, The American
Scholar 58 (1989), 234-244.
B Berndt and S Bhargava, Ramanujan - For
lowbrows, Amer. Math. Monthly 100 (1993),
644-656.
J M Borwein and P B Borwein, Ramanujan and pi,
Scientific American 258 (2) (1988), 66-73.
L Debnath, Srinivasa Ramanujan (1887-1920) : a
centennial tribute, International journal of
mathematical education in science and technology
18 (1987), 821-861.
G H Hardy, The Indian mathematician Ramanujan,
Amer. Math. Monthly 44 (3) (1937), 137-155.
C T Rajagopal, Stray thoughts on Srinivasa
Ramanujan, Math. Teacher (India) 11A (1975),
119-122, and 12 (1976), 138-139.
R A Rankin, Ramanujan's manuscripts and
notebooks, Bull. London Math. Soc. 14 (1982),
81-97.
R A Rankin, Ramanujan's manuscripts and notebooks
II, Bull. London Math. Soc. 21 (1989),
351-365.
R A Rankin, Srinivasa Ramanujan (1887- 1920),
International journal of mathematical education
in science and technology 18 (1987), 861.
R A Rankin, Ramanujan as a patient, Proc. Indian
Ac. Sci. 93 (1984), 79-100
 G.H.Hardy on Ramunujan G.H.Hardy on Ramunujan
Godfrey Hardy was the Cambridge
mathematician who `discovered' the great Indian
mathematician Ramanujan. This is a condensed
version of the first chapter in *Ramanujan : Twelve Lectures on
Subjects Suggested by His Life and Work by
G. H. Hardy (The condensation is courtesy:
Zimath)
Introduction
I have set myself a task that is genuinely
difficult, even impossible --- to form some sort of
reasoned estimate of the most romantic figure in
the recent history of mathematics; a man whose
career seems full of paradoxes and contradictions,
who defies almost all the canons by which we are
accustomed to judge one another, and about whom all
of us will probably agree in one judgement only,
that he was in some sense a very great
mathematician.
The difficulties in judging Ramanujan are clear
--- he was an Indian, I am an Englishman, and the
two parties have always found it hard to understand
one another. He was at best, a half-educated
Indian, since he never could rise to be even a
"failed B.A.". He worked for most of his life
ignorant of modern European maths, and died when he
was thirty and when his mathematical education had
in some ways hardly begun. He published abundantly
(at least 400 pages worth) but left behind even
more unpublished stuff. While this work includes
much that is new, about two-thirds is rediscovery,
that too usually imperfect rediscovery.
His early life
Srinivasa Aiyangar Ramanujan was born in 1887 in
a poor Brahmin family at Erode near Kumbakonam, a
fair sized town in the Tanjore district of Tamil
Nadu. His father was a clerk in a cloth-merchant's
office in Kumbakonam. He was sent at seven to the
local high school and stayed there nine years. By
the time he was in his early teens it was common
knowledge that he was more than just a brilliant
student, discovering for instance the relationship
between circular and exponential functions (cos a +
i sin a = e^ia). This of course had been discovered
by Euler before, as he found out much to his
chagrin later on.
When he was sixteen he came across "A
synopsis of elementary results (actually, over
6000 theorems) in pure and applied
mathematics" by George Carr, . This
enthusiastic book served to introduce Ramanujan to
the real world of mathematics, but in a highly
personal style that relegated the proofs to mere
footnotes. Ramanujan went through the entire book
methodically and excitedly, proving its theorems by
himself, often as he got up in the morn. He claimed
that the goddess of Namakkal inspired him with
formulae in dreams.
His religion
Was he religious? Certainly he observed his
duties as a high-caste Hindu assiduously, like
being a faultless vegetarian and cooking all his
food himself (after changing into his pyjamas
first). And while his excellent Indian biographers
(Seshu Aiyar and Ramachandra Rao) say he believed
in the existence of a Supreme Being, in Kharma,
Nirvana and other Hindu tenets, I suspect he was
not affected by religion any more than as a
collection of rules to be followed. He told me
once, to my surprise, that all religions seemed to
him to be more or less equally true.
Some thought, and may still think, of Ramanujan
as a unintelligible manifestation of the mystic
East. Far from it! He had his oddities, no doubt
mostly originating from his different culture, but
he was as reasonable, sane and shrewd as anyone
I've met. He was a man in whom society could take
pleasure, with whom one could sip tea and discuss
politics or mathematics. He was a normal human
being who happened to be a great mathematician.
The rest of his life
Back to his early days. Thanks to his fine
academic school record, he won a scholarship to
university. But there he spent his time doing
mathematics at the expense of his other subjects,
which he consequently failed. His scholarship was
not renewed. Further attempts to complete his
degree failed. He married at 22 but could not find
a university post, despite the fervent attempts of
some influential Indians he had impressed with his
results, Ramaswami Aiyar and his two biographers.
Finally (at 25) in 1912 he found his first real
job, a mundane clerical one in the Port Trust of
Madras. But the damage had been done --- the years
between 18 and 25 are the critical ones in a
mathematician's life and his genius never again had
the chance of full development. This, and not his
early death, was the real tragedy, that his genius
was misdirected, sidetracked and to some extent
distorted by an inelastic and inefficient
educational system.
But the foundations of at least a partial
recovery had been laid. In 1911 he had published
his first substantial paper and the following year
two Britons, Sir Gilbert Walker and Sir Francis
Spring secured for him a special scholarship (60
pounds a year) that was enough for a married man to
live in tolerable comfort. He wrote to me in early
1913, and Professor Neville and myself got him to
Britain after much difficulty in 1914. He then had
three years of continuous work before falling ill
in mid-1917. He was only able to work spasmodically
(but as well as ever) after this, and died in
1920.
His letters to me
The stories, true and false, of what happened
when I read the letters of an unknown Hindu clerk
have been well spread --- like how I first stored
them in my wastepaper basket before retrieving them
for a second look, and so on. His letters contained
the bare statement of about 120 theorems. Several
of them were known already, others were not. Of
these, some I could prove (after harder work than I
had expected) while others fairly blew me away. I
had never seen the like! Only a mathematician of
the highest class could have written them. They had
to be true, for if they were not, no one would have
the imagination to invent them. A few were
definitely wrong. But that only added credence to
my feeling that the writer was totally honest,
since great mathematicians are commoner than frauds
of the incredible skill that would be needed to
create such a letter.
My collaboration with him While his mind had
been hardened by the time I had access to him,
Ramanujan could still learn new things, and learn
them well. It was impossible to teach him
systematically, but he gradually absorbed new
points of view (like why proofs were important!).
But there were theorems he should have revelled in,
but never used, nor ever seemed to need! The line
between what he learnt from books and learnt for
himself was always very hazy. And here I shall have
to apologize to the world for not asking him about
such matters. For I could have easily asked him,
seeing him daily, and he would have been perfectly
willing to tell me. But I had no idea he was going
to die so soon, and it seemed ridiculous to worry
about how he had found this or that theorem when he
was showing me half a dozen new ones almost every
day.
How good was he?
In his favourite topics, like infinite series
and continued fractions, he had no equal this
century. His insight into algebraic formulae, often
(and unusually) brought about by considering
numerical examples, was truly amazing. But in
analytic number theory, a subject he is often
associated with, I do not believe he actually knew
that much. He certainly contributed little of
significance that was not known already. And in a
subject that relied so much on proof, a subject
where intuition had a bad habit of coming unstuck,
he produced much that was false.
I have in the past tried to say things like "his
failure was more wonderful than any of his
triumphs", but that is absurd. It is no use trying
to pretend that failure is something else. All we
can say is that his failures give us additional,
surprising evidence of his imagination and
versatility. And we can respect him as one who let
his mind run free, instead of keeping it under
saddle and blinkers like so many others do.
Conclusion
But the reputation of a mathematician cannot be
made by failures or by rediscoveries; it must rest
primarily, and rightly, on actual and original
achievement. And it is still possible to justify
Ramanujan on these grounds.
 Biographical Song on Ramanujan
-
Biographical Song on Ramanujan
-
 Words and Music by Mark
Engelberg Words and Music by Mark
Engelberg
- Performed by Mark Engelberg
[Lyrics in PDF]
SECTION 1
In 1887, in the town of Kumbakonam
A baby boy, Ramanujan, was born.
His mom knew in her heart,
From the stars she could chart,
This was no ordinary mind.
The boy grew and played,
While the mother sat and prayed,
Namagiri give us guidance and strength.
With each passing year,
It grew increasingly clear
This was no ordinary mind.
The teachers at school,
Didn't know what to do
With this young man, so many years ahead.
One gave him a math book by Carr -
5000 equations to explore.
For better or worse, a blessing may be a
curse.
He lost interest in everything but math.
SECTION 2
His notebooks filled with formulasthat
no one had conceived;
but his college courses suffered,so he was asked
to leave.
His mother arranged him a marriage
To eleven-year old Janaki.
Now he had to beg for a job
To feed his new family.
Boarded a train bound for Madras
Leaving his family, his new wife, far behind.
Showed his notebook to Inida's brightest
Hoping to find, at last, another brilliant
mind.
Someone who'd understand… his
math…
The math was too far above them
And so his spirits sank.
They had no way to determine
Was he a genius or a crank?
And so he sent out letters
To those who might understand
Twas Hardy who finally recognized
The brilliance of this man.
He'd found someone to understand… his
math…
Boarded a ship, bound for Cambridge
Leaving his country, his people, so far
behind.
Thus began math's most famous collaboration,
Between these two extraordinary minds.
SECTION 3
Hardy welcomed him to Cambridge.
Helping his talent to take wing.
But among his skills there was a weakness:
He had never learned how to prove things.
Ramanujan's conjectures were ingenious
Despite all the gaps in his knowledge.
With Hardy supplying the details and proofs,
The results were astounding.
His insights on continued fractions,
Primes, and diverging series
Dazzled the best mathematicians,
Alluding to brand new theories.
And with each new paper he published,
He was one step closer to fame,
Fulfilling his secret desire,
That the world would remember his name.
Srinivasa Ramanujan (4x)
Cut off from his home and his loved ones,
He felt an acute isolation.
The respect he had earned from his colleagues
At times seemed a small consolation.
And with England weather so dreary,
His body was wasting away.
While hospitalized for consumption,
The royal society honored his name.
Srinivasa Ramanujan (8x)
SECTION 4
In 1919, his health was so poor,
It was finally time to make the journey home.
To spend his final days in the town of
Kumbakonam,
With the bride he'd hardly known.
The last year of his life,
While nursed by his wife,
He recorded 600 new ideas.
To this very day,
His notebooks remain
A source of equations to explore.
And one thing's for sure,
Though his life was cut short,
The world will remember his name.
 Book Review by Krishnaswami Alladi
Book Review by Krishnaswami Alladi
*The Man Who Knew Infinity: A Life of
the Genius Ramanujan - Robert Kanigel, 438pp.
Charles Scribners 1991
The life story of Srinivasa Ramanujan
(1887-1920), the legendary mathematician from
India, is astonishing in many ways. Without any
formal training he produced results of incredible
depth and beauty that challenged some of the finest
minds in England during the beginning of this
century. What is even more remarkable is that he
discovered many of these results while in South
India, where the traditional Hindu way of life had
changed little over the centuries. professor G H
Hardy of Cambridge University was immensely
impressed by these discoveries and arranged for
Ramanujan to go to England. Although Ramanujan had
great difficulties in adjusting to the British way
of life, he wrote several fundamental papers in
Cambridge. But the rigors of life in England during
World War 1, combined with his own peculiar habits,
led to a rapid decline in his health. This forced
him to return to India, where he died a year
later.
Even from his deathbed Ramanujan made startling
discoveries on mock theta functions, about which I
shall comment later. During his all-too-brief life
of 32 years, he left numerous results that were
unique in their beauty, deep, fundamental and of
lasting value; together they place him among the
greatest mathematicians in history. Hardy published
12 elegant lectures in 1940 explaining many facets
of Ramanujan's work; in the past few decades, the
American mathematicians George Andrews, Richard
Askey and Bruce Berndt have published several books
and monographs expanding on Ramanujan's ideas. But
this is the first detailed biography of Ramanujan,
and Robert Kanigel is successful in bringing out
Ramanujan's drama in a most interesting manner.
Ramanujan was born on December 22, 1887, in an
orthodox South India Brahmin family. His parents,
who lived in Kumbakonam, a small town in what is
now the state of Tamil Nadu, had been childless for
many years. They prayed to the Goddess Namagiri,
the deity in the neighbouring town of Nammakkal, to
bless them with a child. Promptly Ramanujan's
mother became pregnant and gave birth in the nearby
town of Erode, her mother's place. To his parents
Ramanujan was a divine gift, and the goddess of
Namakkal was held in great veneration by his
family. Ramanujan grew up in a traditional Hindu
environment, learning stories from the great epics
and verses from the Hindu holy scriptures.
Ramanujan showed signs of his special
mathematical talent early. He kept notebooks in
which he would regularly jot down his findings.
What was most strange was the manner in which he
arrived at his results, and this still remains a
mystery. Often, he would suddenly get up in the
middle of the night and immediately write down
identities involving infinite series and products.
Those near him have said that Ramanujan used to
mention that the Goddess of Namakkal appeared to
him in his dreams and presented him with these
incredible formulae. As an agnostic, Ramanujan's
mentor, Hardy, dismissed the story of the goddess
as mere fable. That such divine inspiration is
often considered to be the cause of work of
exceptionally high quality, however, is more
acceptable to a Hindu than to someone steeped in
Western tradition. For instance, Hindus believe
that it was the blessing of Goddess Kali that
instantly transformed Kalidasa from a shepherd to a
poet par excellence!
During his school years, Ramanujan's excessive
preoccupation with mathematics led to his neglect
of other subjects, and he had to drop out of
college. In 1909, with the intention of making him
more responsible, Ramanujan's mother arranged to
have him married to Janaki, who was then only a
nine-year-old girl.
Next, Kanigel describes Ramanujan's efforts in
approaching influential people for financial
assistance so that he could pursue his research
unhindered by the distractions of a job. What
Ramanujan really needed was the attention of a
leading mathematician. India was a British colony,
and so it was natural for him to write letters to
British professors stating his results. And it was
Hardy who responded favourably.
G H Hardy was, at the beginning of this century,
leading the revival of British mathematicians,
which had taken a back seat in the post-Newtonian
era. Because he was well-known, Hardy was used to
receiving letters from amateur mathematicians who
made false claims about the solutions of famous
problems. So in January 1913, when a letter from
Ramanujan arrived containing a long list of
formulae without any proofs, Hardy's first reaction
was to ignore the letter as one written by a fraud.
However, a closer look showed that there were
several beautiful formulae, some of which defeated
him completely. Hardy cam to the conclusion that it
was more probable that Ramanujan was a genius,
because a fraud would not have had the imagination
to invent such identities! A correspondence
followed, and Hardy invited Ramanujan to Cambridge
so that his raw, untutored genius could be given a
sense of direction.
Both Ramanujan's reaction to this invitation and
his mother's were negative. At that time, orthodox
Hindus believed that it was sinful to cross the
seas. Once again the Goddess of Namakkal provided
the solution! This time his mother had a dream in
which she saw Ramanujan being honoured in an
assembly of European mathematicians, and the
goddess instructed her not to stand in the way of
her son's recognition. So, finally, Ramanujan
sailed for England in 1914. Ramanujan's reluctance
to go to England without his mother's permission
was a typical Hindu reaction. It is a common
practice in India, even today, to seek the
blessings of elders before embarking on a
voyage.
During his few years in England, the rise of
Ramanujan's reputation was meteoric. In each of his
frequent discussions with Hardy, he showed several
new results. For example, under Ramanujan's magical
hand, the theory of partitians that had been
founded by Euler underwent a glorious
transformation. Ramanujan discovered several
astonishing new theorems on partitions involving
congruences and continued fractions. In
collaboration with Hardy, he showed how to obtain
an accurate formula for the number of partitions of
an integer. This is the famous circle method so
widely used in number theory today. In another
paper with Hardy, he began the investigation of
round numbers that led to the creation of
probalistic number theory several years later by
mathematicians such as Paul Erdos. His research was
so impressive that he was elected a Fellow of The
Royal Society (F R S) in 1918.
Ramanujan, who was a gregarious and orthodox
Brahmin, found himself in an awkward position amid
educated Englishmen who were aloof. Socially, Hardy
was the opposite of Ramanujan. This book is a dual
biography, of Ramanujan and Hardy, and Kanigel
succeeds wonderfully in showing the gulf that
separated the two. What bridged this gap was
mathematics, but here too they differed
considerably in the way they thought. Ramanujan was
a genius who conjectured and made giant leaps of
imagination; as a seasoned mathematician, Hardy put
emphasis on rigor and proceeded by logical
step-by-step reasoning.
England's climate proved disastrous for
Ramanujan's health. He never adjusted to the cold
weather. He was in and out of sanatoriums, being
treated mainly for tuberculosis. Having been used
to the curries and spices of India, he found
English to be tasteless. In 1919 his health became
so bad that he returned to India. He died the
following April in Madras.
Hardy felt that the real tragedy was not
Ramanujan's early death, but the fact that he had
wasted much time in India rediscovering past work.
He argued that the best creative work is done when
one is very young and, therefore, that at the time
of his death, Ramanujan was perhaps already pas his
prime. But here Hardy may have been wrong.
Ramanujan's now-famous work on the mock theta
functions was done during his last few months in
India. He wrote one last letter to Hardy
summarizing his discoveries. They are now
considered to be among his deepest contributions.
Ramanujan was definitely on the rise, and he could
have reached even greater heights had he lived
longer.
Hardy compared Ramanujan to Euler and Jacobi as
a genius. Yet he was of the opinion that
Ramanujan's work was strange, and that it lacked
the simplicity of the very greatest works. With
recent advances in the theory of modular forms and
the research of Andrews on Ramanujan's "Lost
Notebook", we now realize that Ramanujan's work is
more fundamental than Hardy had ever imagined.
Ramanujan's equations are now being used to compute
pi (the ratio of the circumference of a circle to
its diameter) to a billion digits! Atle Selberg of
the Institute for Advanced Study at Princeton has
said that it will take many more decades, possibly
more than a century, to fully understand
Ramanujan's contributions.
The fascinating story of the discovery of the
"Lost Notebook" is described in this book. Shortly
after Ramanujan's death, his widow, Janaki,
collected all the loose sheets on which Ramanujan
had scribbled mathematics and sent them to hardy.
They contained more than 600 formulae, including
many on mock theta functions. Hardy handed this
manuscript to G N Watson, who wrote two papers on
this topic. After Watson's death this manuscript
was placed along with Watson's papers at the Wren
Library in Cambridge University, and the
mathematical world remained unaware of its
significance. In 1976, however, Andrews stumbled
across the manuscript while doing some reference
work at Cambridge University. He recognized it
instantly as a priceless treasure and has been
analyzing its contents ever since.
When Ramanujan's centenary was celebrated in
India in december 1987, mathematicians from all
over the world came to pay homage to this legendary
genius. There were several conferences held in
India, of which two were in Madras. The first of
these was at Anna University, for which Andrews had
come in connection with a session on number theory
that I organized. Mrs Ramanujan, who was 87 years
old, was present on the opening day. Kanigel says
"Andrews, his voice choked with emotion, presented
Janaki with a shawl. It was she who deserved the
credit for the Lost Notebook, he said, since it was
she who kept it together while Ramanujan lay
dying." At the second conference, India's prime
minister, Rajiv Gandhi, presented two copies of the
"Lost Notebook", the first one to Mrs Ramanujan and
the other to George Andrews.
Bruce Berndt is editing the notebooks of
Ramanujan. He has published three volumes, and two
more are forthcoming. Andrews and Berndt have plans
to edit the "Lost Notebook". Owing to the efforts
of Andrews, Askey and Berndt, it is now possible to
include Ramanujan's work as part of the regular
graduate mathematics curriculum. And, by reading
this fascinating biography, students will be drawn
to a study of Ramanujan's spectacular results.

Ramanujan's "Lost Notebook" Astounds
Americans
Francis C. Assisi,18
February 2005
Death snatched India's Srinivasa
Ramanujan when his genius had just blossomed - at
age 32 in 1920. Eighty-five years later, it's still
taking several expert mathematicians in America a
lifetime to decipher just a portion of his
incandescent genius. Remarkably too, some of that
work is getting financial support from the National
Security Agency.
Just consider what's happening now. Prof. George
Andrews of Pennsylvania State University, one of
the world's most eminent mathematicians, is
conducting a series of seminars from January 25
until March 22, 2005 at the University of Florida.
Andrews, who has spent the past 30 years studying
Ramanujan's considerable output, is providing
insights into 'Number Theory and Combinatorics'
through six lectures on topics related to
Ramanujan's 'Lost Notebook.' The lost notebook
arises from the last year of Ramanujan's life and
contains approximately 650 assertions without
proofs.
According to Prof. Krishnaswami
Alladi, Chairman of the Department of Mathematics
at the University of Florida, who recently visited
Ramanujan's birthplace, along with Prof Andrews,
the lectures will seek to unveil 'what did
Ramanujan have up his sleeve?' Alladi's research is
in Number Theory, an area where Ramanujan has made
spectacular contributions. He is also the
Editor-in-Chief of The Ramanujan Journal, an
international publication devoted to all areas of
mathematics influenced by Ramanujan.
In his introduction to the first seminar on January
15th, Andrews described the life of Ramanujan, the
discovery of his Lost Notebook, and attempted to
describe some of his surprising achievements. The
third lecture was delivered on February 15. Three
more are scheduled.
Essentially, Ramanujan's legacy consists of 4,000
formulas on 400 pages filling 3 volumes of notes,
all densely packed with theorems of incredible
power but without any commentary or, which is more
frustrating, any proof. In 1976, however, a new
discovery was made. One hundred and thirty pages of
scrap paper, containing the output of the last year
of his life, was discovered by accident in a box at
Trinity College. This is now called Ramanujan's
"Lost Notebook."
Commenting on the Lost Notebook, mathematician
Richard Askey says, "The work of that one year,
while he was dying, was the equivalent of a
lifetime of work for a very great mathematician.
What he accomplished was unbelievable. If it were a
novel, nobody would believe it." To underscore the
difficulty of the arduous task of deciphering the
"notebooks," mathematician Jonathan Borwein and
Peter Borwein have commented, "To our knowledge no
mathematical redaction of this scope or difficulty
has ever been attempted."
Prof. Andrews shot to fame in the 1970s when he
discovered Ramanujan's Lost Notebook at the Wren
Library in Cambridge University and wrote a series
of important papers in Advances in Mathematics in
which he explained Ramanujan's spectacular results
in the context of current research, and in that
process made fundamental improvements as well.
"There is still much to understand about the
implications of many results in the Lost Notebook
and their connections with current research which
is one of the reasons to edit the Lost Notebook,"
said Professor Andrews. The first of these volumes
will appear in 2005 and at least two more volumes
will be forthcoming. "The mathematical content of
the Lost Notebook is so immense, that it is
difficult to predict at this time how many volumes
it will take to completely edit it," he added.
According to Prof. Alladi, during the 1987
Ramanujan Centennial, the printed form of
Ramanujan's Lost Notebook by Springer-Narosa was
released by Prime Minister Rajiv Gandhi, who
presented the first copy to Janaki Ammal Ramanujan,
the late widow of Srinivasa Ramanujan, and the
second copy to Professor Andrews in recognition of
his contributions.
Ramanujan's mathematical wizardry is also the
reason why University of Illinois Prof. Bruce
Berndt, an analytic number theorist with strong
interests in several related areas of classical
analysis, has devoted 31 years of his research to
proving the claims left in three notebooks and a
"lost notebook" by the Indian genius upon his death
in 1920. Twenty-one students have completed
doctoral theses under Berndt's direction, and
currently, five Ph.D. students are writing their
dissertations under his direction. Most are
focusing on material in the lost notebook or on
research inspired by Ramanujan.
The three original notebooks contain approximately
3300 results. The project of finding proofs for
these claims took Berndt over twenty years to
accomplish, and an account of this work can be
found in his books, Ramanujan's Notebooks, Parts
I-V, published by Springer--Verlag in the years
1985, 1989, 1991, 1994, and 1998. Also during this
time, Berndt and Robert A. Rankin wrote Ramanujan
Letters and Commentary and Ramanujan Essays and
Surveys, both published jointly by the American and
London Mathematical Societies in 2001.
Berndt's research in this direction continues, as
he and Andrews plan to publish volumes on
Ramanujan's "lost" notebook, analogous to those
published on the ordinary notebooks. They are
currently "editing" Ramanujan's Lost Notebook,
which will be published by Springer later this
year.
When an interviewer for Frontline asked Brendt if
he found any of Ramanujan's results difficult to
decipher, he admitted: "Oh yes. I get stuck all the
time. At times I have no idea where these formulae
are coming from. … There are times I would
think of a formula over for about six months or
even a year, not getting anywhere. Even now there
are times when we wonder how Ramanujan was ever led
to the formulae. There has to be some chain of
reasoning to lead him to think that there might be
a theorem there. But often n this is missing. To
begin with, the formulae look strange but over time
we understand where they fit in and how important
they are than they were previously thought to
be."
Ramanujan's Passion
Born in India in 1887, Ramanujan
was a mathematical genius whose work continues to
surprise mathematicians into the 21st century. His
work is filled with surprises. At the Ramanujan
centenary conference at the University of Illinois,
it was physicist Freeman Dyson who proclaimed,
"That was the wonderful thing about Ramanujan. He
discovered so much, and yet he left so much more in
his garden for other people to discover."
Born into poverty, Ramanujan grew up in southern
India, and although he had little formal training
in mathematics, he became hooked on mathematics. He
spent the years between 1903 and 1913 cramming
notebooks with page after page of mathematical
formulas and relationships that he had
uncovered.
Ramanujan's life as a professional mathematician
began in 1914 when he accepted an invitation from
the prominent British mathematician G.H. Hardy to
come to Cambridge University. He spent 5 years in
England, publishing many papers and achieving
international recognition for his mathematical
research.
Though his work was cut short by a mysterious
illness that brought him back to India for the
final year of his life, Ramanujan's work has
remained a subject of considerable interest.
The 600 formulae that Ramanujan jotted down on
loose sheets of paper during the one year he was in
India, after he returned from Cambridge, are the
contents of the `Lost' Note Book found by Andrews
in 1976. He was ailing throughout that one year
after his return from England (March 1919 - April
26, 1920). The last and only letter he wrote to
Prof. Hardy, from India, after his return, in Jan.
1920, four months before his demise, contained no
news about his declining health but only
information about his latest work: ``I discovered
very interesting functions recently which I call
`Mock' theta-functions. Unlike the `False'
theta-functions (studied partially by Prof. Rogers
in his interesting paper) they enter into
mathematics as beautifully as ordinary
theta-functions. I am sending you with this letter
some examples ... ''.
The following observation of Richard Askey is
noteworthy: ``Try to imagine the quality of
Ramanujan's mind, one which drove him to work
unceasingly while deathly ill, and one great enough
to grow deeper while his body became weaker. I
stand in awe of his accomplishments; understanding
is beyond me. We would admire any mathematician
whose life's work was half of what Ramanujan found
in the last year of his life while he was
dying''.
As for his place in the world of Mathematics, this
is what Berndt says: `` Suppose that we rate
mathematicians on the basis of pure talent on a
scale from 0 to 100, Hardy gave himself a score of
25, Littlewood 30, Hilbert 80 and Ramanujan
100''.
In 1957, with monetary assistance from Sir Dadabai
Naoroji Trust, at the instance of Professors Homi J
Bhabha and K. Chandrasekaran, the Tata institute of
Fundamental Research published a facsimile edition
of the Notebooks of Ramanujan in two volumes, with
just an introductory para about them.
The formidable task of truly editing the Notebooks
was taken up in right earnest by Berndt in May 1977
and his dedicated efforts for nearly two decades
has resulted in the Ramanujan's Notebooks published
by Springer-Verlag in five Parts, the first of
which appeared in 1985.
Between 1903 and 1914, before Ramanujan went to
Cambridge, he compiled 3,542 theorems in the
notebooks. Most of the time Ramanujan provided only
the results and not the proof. Berndt says: "This
is perhaps because for him paper was unaffordable
and so he worked on a slate and recorded the
results in his notebooks without the proofs, and
not because he got the results in a flash."
The three original Ramanujan Notebooks are with the
Library of the University of Madras, some of the
correspondence, papers/letters on or about
Ramanujan are with the National Archives at New
Delhi and the Tamil Nadu Archives, and a large
number of his letters and connected
papers/correspondence and notes are with the Wren
Library of Trinity College, Cambridge. The
Ramanujan Institute for Advanced Study in
Mathematics of the University of Madras is situated
at a short distance from the famed Marina Beach and
is close to the Administrative Buildings of the
University and its Library. Mrs. Janakiammal
Ramanujan, the widow of Ramanujan, lived close to
the University's Marina Campus and died on April
13, 1994. A bust of Ramanujan, sculpted by Paul
Granlund was presented to her and is now with her
adopted son Mr. W. Narayanan, living in Triplicane
near Chennai.
Ramanujan's story has been told recently by
mathematician Ian Stewart, writing in the magazine
"New Scientist". Stewart brings out strongly the
special nature of Ramanujan's genius, which is his
amazing intuition of the correctness of a
complicated mathematical result. He points out what
a lot this has to do with Ramanujan's lack of a
formal education. Because of this, many of
Ramanujan's proofs have serious gaps in them. They
do not follow step by step in the way that a
conventional proof would. In fact, later
mathematicians have often had to wrestle long and
hard to produce proofs that are completely
watertight: to dot all the i's, and cross all the
t's, as it were. The incredible thing is that for
all their lack of technical rigor, almost all of
Ramanujan's results turned out to be correct.
Alladi says that his visit to Ramanaujam's
birthplace was a dream come true. "What an
inspiration to see this small humble home from
where so many significant mathematical discoveries
poured forth " says Alladi. He informs that
Shanmugha Arts, Science, Technology and Research
Academy (SASTRA), a private university whose main
campus is located in the town of Tanjore, purchased
the home of Ramanujan in 2003, and has since
maintained it as a museum. Research chairs
established at the SASTRA centre at Kumbakonam -
two by the Department of Science and Technology,
Government of India and one by City Union Bank Ltd.
- encourage research in the field of mathematics in
honor of Ramanujan.
Meanwhile the founding has been
announced of the "Ramanujan Prize for Young
Mathematicians from Developing Countries" by the
Abdus Salam International Centre for Theoretical
Physics (ICTP), Trieste, Italy, in cooperation with
IMU, and with support from the Niels Henrik Abel
Memorial Fund, Norway. The Prize will be awarded
annually for the highest mathematical achievement
by young researchers from developing countries,
which conduct their research in a developing
country. The recipient must be less than 45 years
old. Work in any branch of the mathematical
sciences is eligible for the prize. The Prize
amount will be $10,000. The goal is to make the
selection of the first Prizewinner in 2005.
|